Unsere Umgebung ist voll von Signalen, die wir wahrnehmen, z.B. Musik, Licht oder Temperatur, um nur einige Beispiele zu erwähnen. Diese Signale liegen jedoch in analoger Form vor, die heutzutage von zahlreichen Systemen verarbeitet werden müssen, um etwa die Raumtemperatur zu überwachen und gegebenenfalls Alarm zu geben. Wegen der schnell fortschreitenden Entwicklung der Digitaltechnik gewinnt deshalb ein neues Gebiet immer mehr an Interesse: Die digitale Signalverarbeitung (engl.: Digital Signal Processing).
Gerade in der heutigen hochtechnologisierten Welt werden immer schnellere und leistungsfähigere Prozessoren entwickelt, die immer mehr digitale Signale verarbeiten können und somit neue Anwendungsgebiete ermöglichen. Der so genannte Digitale Signalprozessor (DSP) stellt also ein Werkzeug zur digitalen Signalverarbeitung zur Verfügung.
Das einzige Hilfsmittel, um Simulationen von analogen Signalverarbeitungssystemen durchzuführen, war der Digitalcomputer, und damit fing nun die Entwicklung der Digitalen Signalverarbeitung letztendlich an. Die Ingenieure der 60er und frühen 70er Jahre hatten wenig Ahnung, dass ihre Arbeit ein wesentlicher Anteil der digitalen Elektronik für die 90er Jahre und danach darstellen würde.
Digitale Signalverarbeitung war stark abhängig von den Digitalcomputern und der Mehrzahl der Mathematik oder der Algorithmen, die bis 1950 entwickelt wurden. Viele gebräuchliche Algorithmen, die man in der digitalen Signalverarbeitung benutzt, beruhen auf mathematischen Modellen, wie z.B. die Laplace und Fourier Transformationen, die bereits im 19. Jahrhundert vorhanden waren. Sobald die Algorithmen zur Verfügung standen, machten sich die Designer sofort daran, diese auf einer möglichst geeigneten Plattform, in möglichst akzeptabler Zeit laufen zu lassen. Es steht jedoch nicht fest, wann genau der Gedanke aufkam, wirklich digitale Signalverarbeitung anstatt von Simulationen auf Digitalcomputern zu betreiben. Das ultimative Ziel war es, Echtzeit DSP zu erreichen, was aber die ersten Systeme nicht schafften. Sie speicherten die Samples im Hauptspeicher und verarbeiteten diese später.
Hauptarchitekturen für Computer und Single-Chip Microcomputer teilt man in zwei Kategorien. Die Architektur des ersten bedeutenden elektromechanischen Computers hatte getrennte Speicherplätze für die Programme und für die Daten, so dass auf diese parallel zugegriffen werden konnte. Dies ist auch bekannt als Harvard Architektur, die Ende der 30er Jahre von Howard Hathaway Aiken an der Harvard Universität entwickelt wurde. Der Harvard Mark I Computer, auch bekannt als IBM ASCC, arbeitete dann 1944. Die ENIAC (Electronic Numerical Integrator and Calculator) war der erste General-Purpose Computer, der 1943-1946 an der Universität von Pennsylvenien gebaut wurde und ähnlich der Architektur des Harvard Mark I war. Wegen der Komplexität der getrennten Speichersysteme wurde diese Architektur jedoch nie sehr populär bei General-Purpose Computern. Deswegen entwickelte John von Neumann, einer der Berater des ENIAC-Projektes, eine Architektur, die mit nur einem Speicher für Befehle und Daten auskam: Die Von Neumann-Architektur. Seine Idee war es, dass die Instruktionen in zwei Hauptgebiete aufgeteilt werden können: Die Operation und die Adresse des Operanden. Der erste Computer mit dieser Architektur war der IAS (1951). Mit dieser Architektur wurde das Design vereinfacht, auf Kosten einer Einschränkung: In einem Instruktionszyklus konnte man entweder auf den Befehl oder auf die Daten zugreifen. Die Geschichte zeigt, dass diese Einschränkung bei General-Purpose Computern dennoch ausreicht. Die Intel i86 Familie sowie viele andere Computer der kommenden 40 Jahre nutzten z.B. diese Architektur. Die Berechnungsblöcke waren die ALU (Arithemetic Logic Unit) und ein Shifter. Operationen wie Add, Move und Subtraktionen wurden sehr einfach in wenigen Taktzyklen erledigt. Komplexere Befehle wie Multiplikationen und Divisionen wurden aus einer Serie von einfachen Shift-, Add- oder Subtraktions-Befehlen erzeugt. Geräte mit einem komplexen Befehlssatz nennt man auch CISC (Complex Instruction Set Computers) Geräte. Diese CISCs sind ungeeignet für die digitale Signalverarbeitung, da sie in Bezug auf Multiplikationen sehr langsam sind. DSP-Algorithmen berechnen oft Daten in der Form A = B * C + D.
1971 entwickelte Lincoln Laboratories den Lincoln FDP (Fast Digital Processor). Er führte Multiplikationen in 600 Nanosekunden aus, wurde aber von 10000 einzelnen ICs gebaut. Sein Problem war die Von Neumann Architektur. Als Nachfolger dieses Prozessors erschien dann der Lincoln LSP/2, der dann eine ähnliche Architektur wie der Harvard I Computer aufwies. Mit diesem war es dann möglich viermal so schnell wie der FDP zu sein, aber nur mit ein Drittel der ICs auszukommen. Später entwickelten andere Forschungsinstitutionen Signalverarbeitungscomputer mit 200 ns pro Multiplikation, die sogar echtzeitfähig waren. Mit der zunehmenden Technologisierung war es dann in den ersten Jahren um 1980 dann soweit, dass die ersten Single-Chip Digital Prozessoren das Licht der Welt erblickten: AMI S2811, Intel 2920, NEC µPD7720 und dann der TMS32010 von Texas Instrument. Letzterer gilt als der Durchbruch der DSPs überhaupt, da dieser schon mit assembler-ähnlichen Befehlen programmiert werden konnte, während der AMI S2811 beispielsweise noch einen eigenen Mikroprozessor zur Initialisierung und Konfiguration brauchte. Dies ist der Anfang des großen Siegeszuges der heutigen DSP-Technologie.
Doch wie funktioniert überhaupt die digitale Signalverarbeitung? Dazu müssen wir zunächst einmal wissen, welche Signale überhaupt verarbeitet werden können. Anhand einer Grafik werden die vier vorkommenden Signaltypen dargestellt.

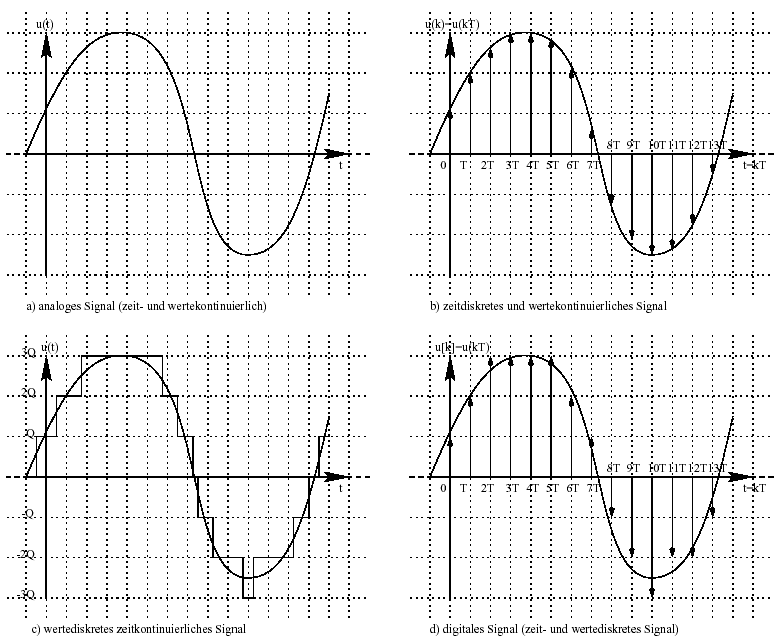
Abbildung 1: Signaltypen
Analogsignal
Wir wissen bereits, dass unsere Umgebung aus analogen Signalen besteht. Ein analoges Signal kann z.B. eine von der Zeit t abhängige Spannung u(t) sein, die aus beliebigen reellen Zahlenwerten besteht. Dieses Signal ist zeit- und wertekontinuierlich. (Abb. 1a)
Zeitdiskretes Signal
Eine unmittelbare Verarbeitung eines analogen Signals mit Hilfe eines Digitalen Signal Prozessors ist jedoch nicht möglich, da dieser nur zu festen Zeitpunkten Messwerte (so genannte Samples) verarbeiten kann. Das Einteilen in äquidistante Zeitabstände bezeichnet man auch als abtasten und macht aus dem zeitkontinuierlichen Signal ein zeitdiskretes. Als Abtastperiode T wird die Zeit zwischen zwei solchen gleichgroßen Abständen bezeichnet. Den Kehrwert der Abtastperiode nennt man dann Abtastfrequenz fa = (1/T). Damit das Eingangssignal am Ausgang des Systems exakt rekonstruiert werden kann, muss die Abtastfrequenz fa mindestens doppelt so groß, wie die größte im Fourierspektrum des Eingangssignals vorkommende Frequenz fmax gewählt werden. Dies folgt aus dem Abtasttheorem von Nyquist und Shannon. Der Anti-Aliasing-Filter dient genau diesem Zweck. Nur die Frequenzanteile des Ursprungssignals, die diesem Theorem genügen, können das Filter passieren.
Wertediskrete Signale
So ähnlich wie bei dem zeitdiskreten Signal kann man auch den Wertebereich des Eingangssignals in äquidistante Abschnitte unterteilen und erhält dadurch ein wertediskretes Signal, das dem auf der diskreten Werteachse jeweils nächsten Wert des Signals zugeordnet wird. Dieser Vorgang wird als Quantisierung bezeichnet, der mit Hilfe eines Analog-Digital-Wandlers durchgeführt wird. Den Fehler, den man bei der Quantisierung macht, nennt man Quantisierungsfehler.
Digitale Signale
Dies sind die einzigen Signale, die ein DSP verarbeiten kann. Digitale Signale sind sowohl zeitdiskret, als auch wertediskret. Es ist die numerische Repräsentation eines analogen Signals (Abb. 1d)
Da man nur digitale Signale verarbeiten kann, müssen diese aus den analogen Signalen generiert werden. Mit folgendem DSP-System wäre es z.B. möglich, einen digitalen Filter zu realisieren (Abb. 2). Durch den Integrationsgrad heutiger ICs kommt man mit nur wenigen Bauteilen aus.
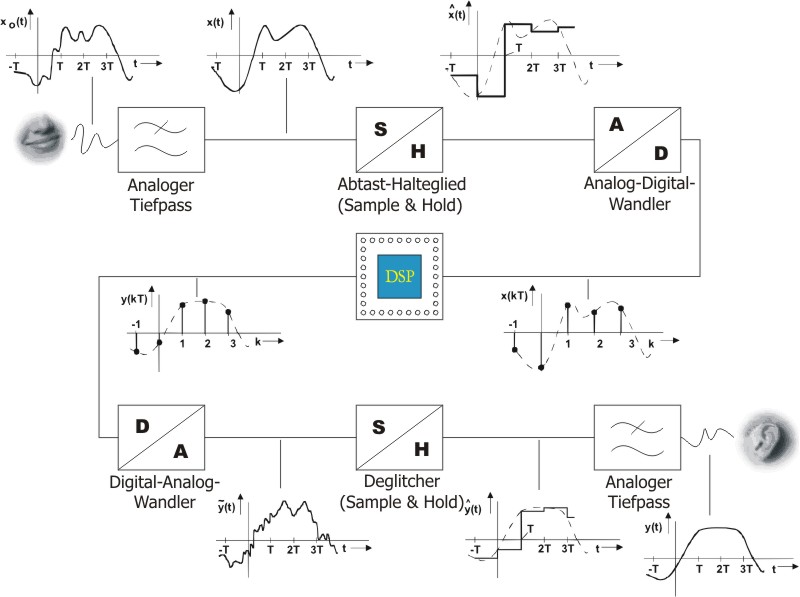
Abbildung 2: DSP-System
Neben dem Signalprozessor (DSP), der die digitale
Signalverarbeitung vornimmt, indem er die Messwerte (Samples) verarbeitet, sind
weitere z. T. sehr aufwendige analoge Komponenten notwendig:
Analog-Digital-Wandler (ADC), Digital-Analog-Wandler (DAC), Abtast-Halteglieder
und Tiefpassfilter.
Das analoge Signal durchläuft zunächst den (analogen) Tiefpassfilter, der dafür
verantwortlich ist, dass diesen nur Signale passieren können, die dem
Abtasttheorem genügen. Das Abtasthalteglied am Eingang hat die Funktion, das
Signal für die Zeitdauer der Analog-Digitalumsetzung konstant zu halten, denn
dies dauert eine gewisse Zeit.
Der so genannte Deglitcher, eine weitere Sample & Hold-Einheit, wird
insbesondere bei hohen Anforderungen an die Güte des Ausgangssignals eingesetzt.
Er entlastet das analoge Tiefpassfilter, indem er das Ausgangssignal des
D/A-Wandlers glättet.
Wie der Begriff Digitaler Signalprozessor schon vermuten lässt, geht es bei DSPs um auf spezielle Aufgaben der digitalen Signalverarbeitung abgestimmte Prozessoren.
Die Einsatzfelder für Digitale Signalprozessoren haben besondere
charakteristische Eigenschaften. Es werden oft wiederholende numerische
Berechnungen durchgeführt, bei denen hohe Anforderungen an die Genauigkeit
gestellt werden. Eine hardware-unterstützte Überlaufkontrolle ist oft sinnvoll.
Es wird oft multipliziert und addiert. Diese Rechenoperationen verlangen eine
schnelle Verfügbarkeit der zur Berechnung benötigten Daten. Eine weitere
wichtige Anforderung ist die schnelle Durchführung von häufigen
Speicherzugriffen auf hintereinanderliegende Speicherbereiche.
Die Addition und Multiplikation sollen möglichst in einem Instruktionszyklus
erfolgen. Es müssen dabei mehrere Operanden geladen sowie außerdem das
Berechnungsergebnis oder einer der Operanden in diesem Zyklus wieder im Speicher
abgelegt werden. Besondere Unterstützung verschiedener Adressierungsarten, z.B.
für die Realisierung von Koeffizientenspeichern, sind erforderlich. Eine
effiziente Realisierung von Schleifen soll möglichst hardware-unterstützt
erfolgen, denn bei vielen Berechnungen steht schon vorher fest, wie oft eine
Schleife durchlaufen werden soll. Das Inkrementieren und Abfragen von
Schleifenzählern kann automatisiert werden. Da viele Daten eingelesen und
ausgelesen werden, muss ein Prozessor, der für solche Anforderungen konzipiert
ist, über leistungsfähige Ein- und Ausgabemöglichkeiten verfügen. Ein geringer
Stromverbrauch ist zusätzlich noch wünschenswert.
Das Gebiet der digitalen Signalverarbeitung ist ein boomender Markt und so ist es auch kaum zu verwundern, dass man schon mit einigen Produkten der heutigen Welt in Berührung gekommen ist. Folgende Anwendungen stellen viele oder alle Forderungen, die wir oben kennen gelernt haben, an den Prozessor:
| Consumerbereich |
| DVD, CD-Player, MP3-Player, Digitales Fernsehen, Videoverarbeitung, Musikverarbeitung, Motorkontrolle und Servosysteme (z.B.: Festplatten, CD-Player), Fax, Waschmaschine |
| Telekommunikation |
| Handy, Pager, xDSL, ISDN, Voice over IP, Modem, UMTS, Wireless LAN, Bluetooth, Satellitenkommunikation, Abhörsichere Kommunikation |
| Automobilbereich |
| ABS, EPS, Kollisionsvermeidung, Aktive Geräuschreduzierung, elektrische Sitze und Spiegel, Motorlaufkontrolle, Parkhilfe, Navigationshilfe, Digitales Radio, Sprachsteuerung, Klimaanlage, Airbag, GPS |
| Industrie |
| Motorkontrolle, Robotik, Computersehen, Servokontrollsysteme, Barcode-Lesegerät, Meßtechnik |
| Militär und Forschung |
| Sonar- und Radarsysteme, Seismische Analyse, Medizinische Ultraschallanwendungen, Raketen Leitsysteme, Flugzeug Kontrollsystem |
Nachdem nun die wichtigsten Blockbuster der DSP-Welt vorgestellt worden sind, wird nun als typische DSP-Anwendung der FIR-Filter vorgestellt. Mit Hilfe eines FIR-Filters (Finite Impulse Response) können beliebige endliche Impulsantworten realisiert werden.
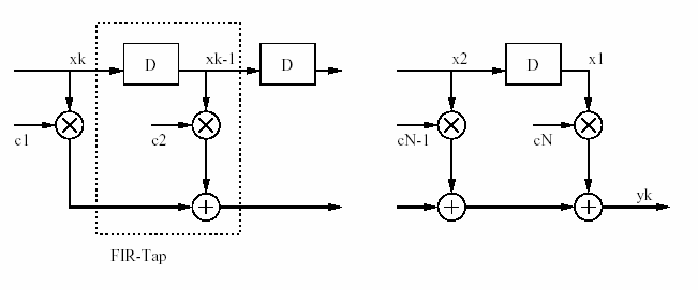
Abbildung 3: FIR-Filter
Die Struktur dieses Filters ist vergleichsweise einfach aufgebaut: Durch die Koeffizienten ci beeinflusst man die Eigenschaften des Filters. Man erkennt dort sehr einfach die typischen Operationen, die zur Realisierung notwendig sind. Der aktuelle Ausgabewert yn des Filters berechnet sich wie folgt:
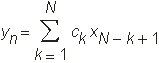
Wird ein neues Sample am Eingang übernommen, so muss aus den N bisher eingegangenen Samples xi und aus den Filterkoeffizienten ci der neue Ausgangswert yn berechnet werden. Dabei wird N-mal addiert und N-mal multipliziert, um das Ergebnis zu berechnen. Die Berechnung muss abgeschlossen sein, bevor das nächste Sample vom Eingang abgegriffen wird. D ist ein Sample & Hold-Glied, das verzögert. Das aktuelle Sample muss nach der Berechnung im Verzögerungsspeicher abgelegt werden, da es zur Berechnung der folgenden Ausgangswerte benötigt wird. Es wird einem schnell klar, dass zum Berechnen eines neuen Ausgangswertes eine große Anzahl von Additionen und Multiplikationen in nur kurzer Zeit durchgeführt werden müssen.
Wie oben schon erwähnt, sind digitale Signalprozessoren auf spezielle Aufgaben der digitalen Signalverarbeitung abgestimmte Prozessoren. Das folgende Blockschaltbild zeigt die wichtigsten Eigenschaften eines solchen DSPs:
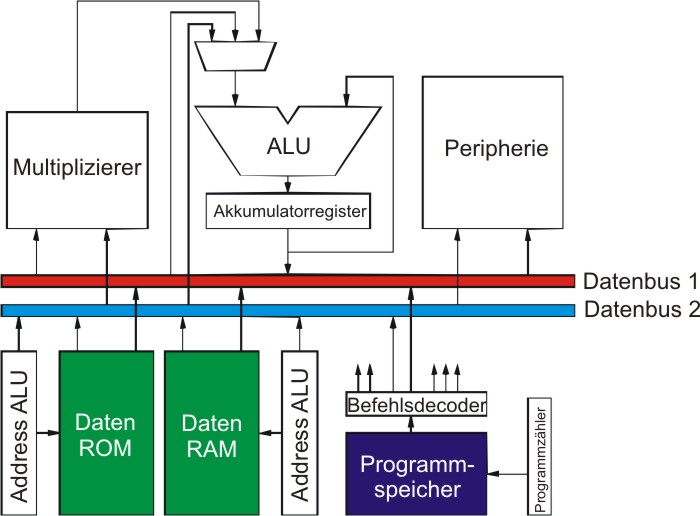
Abbildung 4: Vereinfachtes Blockschaltbild eines Signalprozessors
Deutlich erkennbar ist der getrennte Daten- und Programmspeicher. Der Datenspeicher ist bei diesem Prozessor noch einmal aufgeteilt in Daten-ROM (z.B. für feststehende Filterkoeffizienten) und einem Daten-RAM (z.B. für die aufgenommenen Samples). Die Address-ALU ermöglicht einige interessante Adressierungsarten ohne großen Zeitverlust. Man erkennt deutlich, dass Multiplizierer und Akkumulator in einem gemeinsamen Datenpfad liegen. Dies erlaubt die Ausführung einer Addition und Multiplikation in einem Instruktionszyklus.
MAC-Operation
Die so genannte Multiply-Accumulate-Operation (MAC) ist eine der zentralen
Operationen eines DSP. Sie erlaubt z.B. die Berechnung eines Vektorprodukts,
welches beispielsweise für digitale Filterfunktionen verwendet wird. Das
Vektorprodukt besteht aus einer Summe von Produkten der Vektorelementepaare. In
Maschinencode umgesetzt, bedeutet dies die wiederholte Anwendung der
MAC-Operation in Verbindung mit der Summenbildung.
Um die MAC-Operation in einem Instruktionszyklus berechnen zu können, muss
gewährleistet sein, dass die Multipliziereinheit und ein Akkumulator im
Hauptdatenpfad des DSPs eingebettet ist. Um weiterhin sicherstellen zu können, dass es bei einer Serie von MAC-Operationen nicht zu einem Überlauf des Akkumulators kommt, ist bei den
meisten DSPs dieser mit zusätzlichen Bits versehen.
Speicherorganisation
Zu einem schnellen Gesamtsystem gehören auch schnelle Teilsysteme, und so darf auch die Speicherorganisation kein Nadelöhr des DSPs darstellen. Aus diesem Grund ist ein DSP in der Lage, mehrere Speicherzugriffe in einem Instruktionszyklus gleichzeitig durchzuführen. Parallel zum Holen eines Befehls werden die dazu benötigten Operanden geladen und die Ergebnisse der vorherigen Operation in den Speicher geschrieben. Während der Prozessor die MAC-Operation ausführt, wird parallel dazu der Messwert und der Koeffizient für die Berechnung geladen. Um dies zu ermöglichen, haben viele Signalprozessoren mehrere on-chip Busse, multi-ported on-chip Speicher und manchmal auch mehrere unabhängige Speicherbänke.
Der Name für eine solche Architektur mit getrennten Speicherbereichen für Programmcode und Daten ist Harvard-Architektur im Gegensatz zu der Von Neumann Architektur, die in herkömmlichen Mikroprozessoren Verwendung findet und in der nur ein Speicherbereich für Programm und Daten zur Verfügung steht. Viele neuere DSPs verwenden sogar mehrere getrennte Speicherbereiche für die Daten. Eine solche Anordnung nennt man dann erweiterte Harvard-Architektur.
Adressierungsarten
Damit die Rechengeschwindigkeit noch einmal gesteigert werden kann, werden auf DSPs Adress Generation Units (AGU) eingesetzt. Ohne den Hauptdatenpfad des Prozessors zu nutzen, können die Speicheradressen, z.B. für die Operanden, parallel zu arithmetischen Operationen, wie z.B. der oben erwähnten MAC-Operation, ausgeführt werden. Viele dieser AGUs unterstützen die Register-Indirekte Adressierung mit nachträglicher Inkrementierung, die überall dort eingesetzt werden, wo wiederholte Berechnung auf Daten durchgeführt werden sollen, die sequentiell im Speicher angeordnet sind. Oftmals wird auch eine Modulo Adressierung zur Verfügung gestellt. Einige Prozessoren ermöglichen auch eine Bit-reversed Adressierung, die für manche Fast Fourier Transformations (FFT) Algorithmen eingesetzt werden.
Schleifenbefehle
Manche Prozessoren unterstützen besonders Schleifenbefehle, um die Ausführung von Schleifen zu beschleunigen. Hierbei gibt es Prozessoren, die nur eine Operation wiederholen können oder auch solche, die die Fähigkeit haben, gleich den ganzen Anweisungsblock auf diese Weise zu wiederholen. Man spricht hier von Single- und Multiinstruction Hardware Loops. Solche Schleifen werden von der Hardware kontrolliert ausgeführt. Der Programmierer muss sich weder um die Inkrementierung des Schleifenzählers kümmern, noch um die Abbruchbedingung der Schleife. Einige neuere DSPs verwenden prozessorintern Pipelines und Cachespeicher vergleichbar mit RISC-Prozessoren, um die Schleifenoperationen schneller ausführen zu können.
Kommunikation
Die meisten Prozessoren unterstützen außerdem ein oder mehrere serielle bzw. parallele I/O-Interfaces, Interruptausführung mit geringem Overhead oder DMA (Direct Memory Access), um Datentransporte fast ohne Benutzung des restlichen Prozessors zu gewährleisten.
Signalprozessoren lassen sich in zwei große Familien aufteilen. Diese unterscheiden sich durch ihre interne Zahlendarstellung. Es gibt DSPs mit Festpunkt-Arithmetik und Prozessoren mit Floatingpoint-Arithmetik. Letztere sind in ihrer Anschaffung wesentlich teurer, da sie deutlich komplexer sind und meist in ihrer Rechenleistung den Festpunkt-DSPs überlegen. So wird diese Art von Prozessoren häufig bei zeitkritischen Anwendungen eingesetzt. Da es aber im DSP-Geschäft primär darum geht, den Signalprozessor einzusetzen, der die Anforderungen der Anwendung am besten erfüllt – und hierzu gehört besonders oft der Preis –, werden in den meisten Anwendungsfällen Festpunkt-DSPs eingesetzt.
Doch wie verhält sich nun ein Standard-Prozessor bei DSP-typischen Anwendungen?
Da nun die Besonderheiten eines DSPs erläutert worden sind, soll hier gezeigt werden, wie sich die spezifischen Merkmale eines Signalprozessors bei Assemblerprogrammierung bemerkbar machen.
| General-Purpose-Prozessor
(Abb. 5a): loop: |
Abb. 5a): Datenpfad eines GPCs |
Die zentrale Programmschleife des FIR-Filters auf einem Prozessor mit Von Neumann Architektur mit einem gemeinsamen Speicher für Daten und Programmcode. Aufwendig ist hier die Schleifensteuerung. inc, tst, jnz werden explizit aufgerufen und verbrauchen somit Ausführungszeit. |
| Digitaler Signal Prozessor (Abb. 5b):
move #Xaddr,r0 |
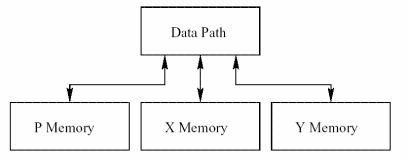 Abb. 5b): Datenpfade des DSPs |
Noch einmal die zentrale Schleife zur Realisierung des FIR-Filters. Es ist deutlich weniger Code nötig. Inkrementierung, Adressierung des Speichers, Schleifenkontrolle wird direkt von der Hardware des DSP erledigt. Laden der Operanden, Berechnen des FIR-Taps geschieht in einem Schritt mit der mac-Anweisung. Hier vergeht nur exakt ein Instruktionszyklus. Auch die Programmierung der Schleife ist deutlich kompakter und effizienter gelöst. |
Geschwindigkeitsvergleiche zwischen verschiedenen Signalprozessoren oder gar zwischen DSP und General-Purpose-Prozessoren besitzen oft nur wenig Aussagekraft. Die Geschwindigkeit eines Prozessors wird von den Herstellern oft in MIPS (Micro-Instructions Per Second), MOPS (Million Operations Per Second) oder MACS (Multiply-Accumulate per Second) angegeben. Keine der genannten Vergleichsangaben berücksichtigt, wie viel sinnvolle Arbeit in einem Instruktionszyklus bzw. während einer Operation verrichtet werden kann, noch die Geschwindigkeit der hierzu benötigten Speicherzugriffe. Außerdem unterscheidet sich der Befehlssatz der Signalprozessoren signifikant, so dass eine Instruktion bei verschiedenen DSPs etwas Unterschiedliches bedeuten kann. Aus diesem Grund bezieht sich der hier angegebene Vergleich von Prozessoren auf einen Benchmark der Berkely Design Technology, Inc. (BDTi). Dort werden spezielle DSP-Algorithmen an die unterschiedlichen Prozessoren angepasst. Deren Ausführungsgeschwindigkeit wird dann verwendet, um einen „objektiveren“ Performancevergleich durchführen zu können.
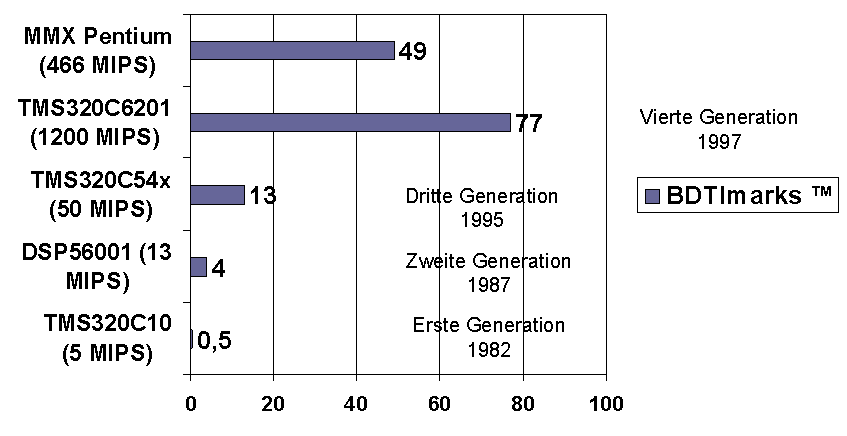
Abbildung 6: Geschwindigkeitsvergleich nach BDTi
Der Einfluss des Erfolges von DSPs im Bereich Sprachcodierung und
Audioverarbeitung macht sich auch bei den General-Purpose-Prozessoren bemerkbar.
So ist z.B. Intels MMX eine Erweiterung dieser Prozessoren um DSP-Fähigkeiten.
Dieser Trend scheint sich auch fortzusetzen. Die Performance leistungsfähiger
General-Purpose-Prozessoren erlaubt es, auf ihnen auch spezifische
DSP-Anwendungen laufen zu lassen. In Zukunft wird man also auch ohne ein
externes Modem auskommen können, denn für DSP angepasste Prozessoren, wie man
sie heute zum Teil in seinem Homecomputer schon besitzt, ist es dann möglich,
per Software die ehemalige Hardware zu ersetzen. Problematisch ist nur die Frage
der Echzeitfähigkeit, denn solche Prozessoren arbeiten oft auf komplexen
Betriebssystemen. In Systemen, bei denen DPS-Funktionalität erforderlich ist und
ein Microcontroller bzw. ein Microprozessor und zusätzlich ein DSP eingesetzt
wird, bietet es sich an, den DSP zugunsten eines leistungsfähigeren
Microcontrollers oder Microprozessors einzusparen. Dies erhöht die
Integrationsdichte und somit auch den Stromverbrauch. Ein Systementwickler
braucht dann nur noch den einen Prozessor zu programmieren, statt vorher
mehrere. Dadurch verkürzt sich auch die Entwicklungszeit.
Die Entwicklungen im Bereich der Digitalen Signalverarbeitung sind rasant. Den
Umsatz mit programmierbaren Signalprozessoren bezifferte die Organisation „World
Semiconductor Trade Statistics“ (WSTS) für das Jahr 2000 mit 6,1 Milliarden
US-Dollar. Im Vergleich zum Vorjahr (1999: 4,4 Milliarden US-Dollar) ist dies
ein Wachstum von 40%. Der gesamte Halbleiter-Markt für alle ICs hatte dagegen
„nur“ ein Wachstum von 35%. Dies ist ein erstes Anzeichen, dass sich die DSPs
langsam auf breiter Basis im Markt zu etablieren scheinen, auch wenn das Jahr
2001 eine starke Delle in der Entwicklung wegen der Kunjukturschwäche darstellt.
Abbildung 7 stellt einen Ausblick der Entwicklung dar.
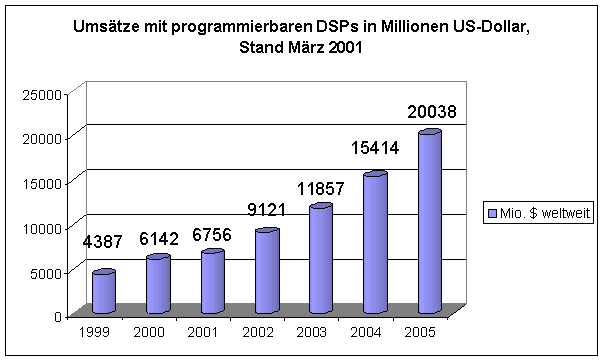
Abbildung 7: Weltweite Umsätze mit programmierbaren DSPs
Hauptabsatzgebiete der DSPs sind weiterhin noch die Handy-Chips,
aber gerade der ADSL-Markt scheint stark im Kommen zu sein. 900%
Absatzsteigerung im Jahr 2000 konnte Texas Instruments in dieser Kategorie
melden. Aber auch der Bereich des Internet-Audios (wie z.B: MP3-Player und
Internet-Telefonie) ist sehr umsatzstark mit 300%. Es ist zu erwarten, dass
Voice-over-IP (VoIP) zukünftig eines der Absatzmärkte überhaupt darstellen wird.
Denn sowohl auf der Seite der Infrastruktur-Ausstatter sowie der Endanwender
werden neue DSP-Chips auf den Markt gebracht, die mehrere VoIP-Kanäle parallel
verarbeiten können. Solche neuen Chips nennt man auch „Access Communication
Chips“ (ACPs).
Fast jedes Zusatzmodul für Personal Digital Assistants (PDAs) basiert
mittlerweile auf DSP-Technologie. Zu nennen wären dort MP3-Player,
GPS-Ortungssysteme, Bluetooth-Tranceiver oder sogar „Handy-Module“.
Die Entwicklung verläuft immer rasanter, die Prozessoren werden immer leistungsfähiger. Zukünftig wird man vermutlich Anwendungen finden können, die heutzutage noch undenkbar sind und die es heißt, mit Hilfe der zukünftigen Technik im Markt zu etablieren.
BIER, J.: The Evolution of DSP Processors. Seminar 1997. –
University of California at Berkeley
http://www.bdti.com/articles/slides.evolution.pdf
BIER, J; Eyre, J.: The Evolution of DSP Processors. Berkeley
Design Technology, Inc. (BDTI), 2000.
http://arch1.cs.ccu.edu.tw/~dsp_arch/Bier_article.pdf
Channel-e – Online-Magazin für Elektronik: DSPs bleiben eine
Schlüsselkomponente, 2001
http://www.channel-e.de/deutsch/news/dsp/dsp-markt-2001.htm
MARVEN, C. & EWERS, G.: A Simple Approach to Digital Signal Processing. Texas Instruments: Alden Press Limited, 1994.
WAGENER, W.; WETTER, O ; SCHNEIDER, M; NÄGER, G.: Digitale Signalprozessoren für Audio. Aachen : Elekor-Verlag, 1994
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Aiken.html